Mi köze a matematikának Dobbléhoz? Egyáltalán létezik-e a Dobble? Valóban végtelen a végtelen sík? Ezek a kérdések kerültek terítékre március 9-én, a Matemorfózis x Speakesy előadáson.
Pintér Gergő, az MTA Rényi Alfréd Matematikai Kutatóintézet tagja, tanít az ELTE-n és a BME-n is, emellett Matemorfózis néven ismeretterjesztő előadásokat szervez például fesztiválokon, vagy éppen kocsmákban. Ahogyan pénteken is elhangzott, ezek a rendezvények kifejezetten nem matematikusoknak szólnak, hanem mindenkinek, aki azt gondolja, hogy ez egy merev szabályrendszerű, földhözragadt tudomány, amiből, ha valaki rossz volt középiskolában akkor ostoba hozzá. És szeretne is mindenkit meggyőzni ennek az ellenkezőjéről.
A pénteki előadás helyszíne a Közkincs Könyvtár volt, ami egy „magánkönyvtár, közösségi tér és találkozási pont.” Az biztos, hogy a Rákóczi úti polgári lakásban berendezett hely otthonos, kedves atmoszférája rögtön egy bensőséges, családias hangulatot teremt a javarészt teljesen idegenekből álló 15-20 fős társaságban, ami megjelent. Nincsen katedra, merev sorok, hanem kanapé, fotel, néhány szék, körben ülés, ötletelés, irányított beszélgetés.

A Közkincs Könyvtár mindent megtesz az otthonosság-érzetért.
a kép forrása: a Közkincs Könyvtár facebook oldala
A téma talán meglepőnek tűnik. Hogyan lehet Dobble-paklit tervezni? És egyáltalán mi köze ennek a matematikához? Aki nem ismerné, a Dobble egy olyan kártyajáték, amelyben minden kártyán 8 darab ábra van, és bármely két kártyán pontosan egy egyforma ábra található, ahogyan azt az alábbi kép is jól szemlélteti. A kérdés már-már nevetségesen egyszerűnek tűnik, de aki nekilát a feladatnak (egy ilyen pakli megtervezésének), az hamar rájön, hogy könnyen zsákutcákba lehet futni, ha az embernek nincsen valami szisztémája. De vajon mi legyen ez a szisztéma? A közös ötletelés során gyorsan előkerülnek a triviális megoldások (például minden kártyára tegyünk mondjuk egy szívet, és aztán még 7 másikat, amelyek különböznek), amikkel sajnos az a baj, hogy temérdek mennyiségű ábrát kéne kitalálni hozzájuk, illetve nem vezetnének izgalmas játékhoz. Ez a rövid brainstorming, majd a csöndes, önálló kísérletezés elegendő volt ahhoz, hogy a társaság kétkedő tagjait is meggyőzze a probléma nehézségéről, és mindenkit kíváncsivá tegyen a végső válaszra.
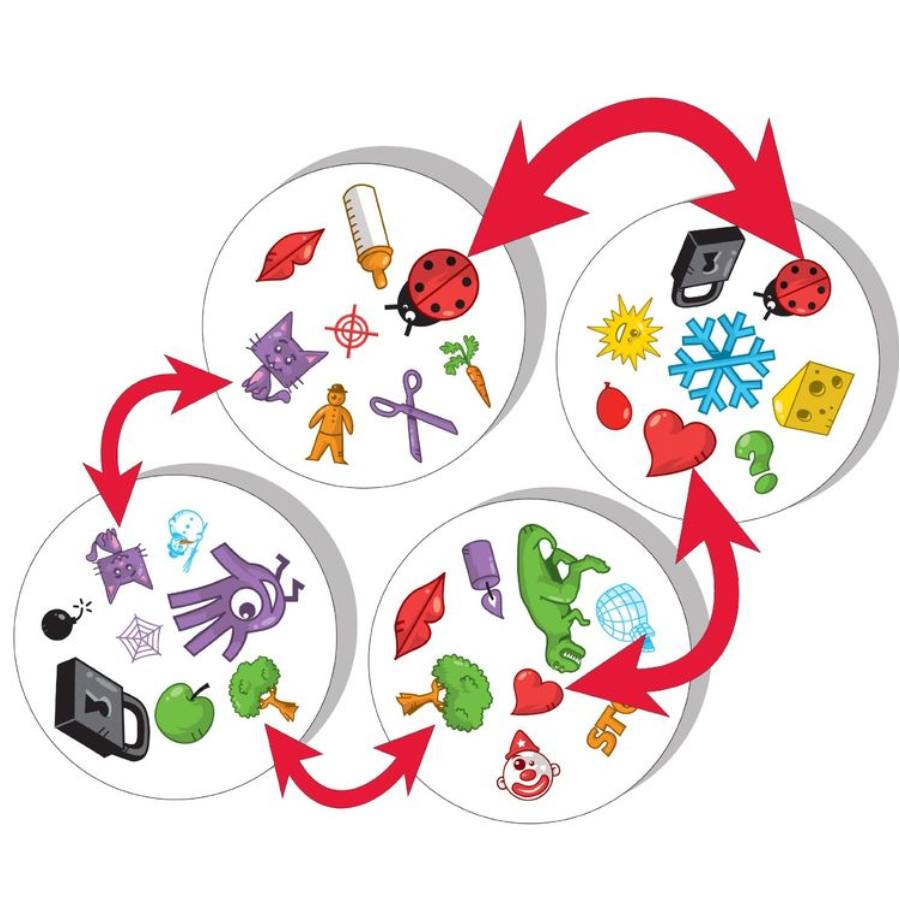
A Dobble-pakliban bármely két kártyán pontosan egy egyforma ábra található.
a kép forrása: az esemény facebook oldala
És itt érkezik meg a matematika a történetbe, de az is egy kis csavarral. Pintér kiemeli, hogy ahhoz, hogy ezt a problémát strukturálni, általánosítani tudjuk, persze jól jönnek a matematikai eszközök, de hogy eljussunk azokig egy olyasfajta gondolkozási módra van szükségünk, amit inkább művészetektől szoktunk meg: asszociációkra. Némi gondolkozás után megfejtjük, hogy a lapokra nem csak az igaz, hogy bármely kettőn egy és csak egy egyforma található, hanem ez is, hogy bármely két ábra együtt, pontosan egy lapon szerepel. Azaz, csak egy olyan lap található, amin rajta van a figurák közül mondjuk a dinoszaurusz és a gyertya. Ebből az következik, hogy bármelyik két lap egyértelműen meghatároz egy ábrát (amelyik közös a két lapon), és bármelyik két ábra egyértelműen meghatároz egy lapot (amelyiken rajta van mindkettő). És itt van szükség az asszociációkra, hogy a homlokunkra csapjunk: de hát akkor az ábrák lehetnének egyenesek, a lapok pedig pontok, hiszen azokra ugyanez elmondható: a síkon bármely két pont (lap) egyértelműen meghatároz egy egyenest (ábrát), és bármely két nem párhuzamos egyenes (ábra), egyértelműen meghatároz egy pontot (lapot). És ahogy felfedeztük ezt a hasonlatot, hirtelen egy könnyebben kezelhető problémát kaptunk, ami nem mellesleg a modern matematika egyik ágának, a diszkrét geometriának a hatásköre. Megállapítottuk, hogy a Dobble-pakli lényegében megfeleltethető egy olyan alakzatnak, egy olyan „világban” (a végtelen síkon), ami tulajdonképpen nem is létezik… Persze az átkötésnek még vannak problémái (mi történik a párhuzamos egyenesekkel, vagy éppen azzal, hogy a síkon végtelen sok pont/egyenes van, míg kártyából nyilvánvalóan véges sok?), de ezeknek a magyarázataiba nem bonyolódnék bele írásban. Legyen elég az alábbi ábra, amin egy 13 lapos “Dobble-pakli” szerepel. Ha minden egyeneshez választunk egy figurát, akkor ez alapján már játszi könnyedséggel meg tudjuk tervezni a játékot. Hiszen, minden metszéspont egy kártyalap lesz, amire azok a figurák fognak kerülni, amiket az adott ponton áthaladó egyenesek “jelentenek.” Végezetül még közösen kirakjuk az alábbi ábra 57 ponttal rendelkező “változatát”, ami az a “nemlétező” alakzat, ami pont megfelel a Dobble-paklinak.
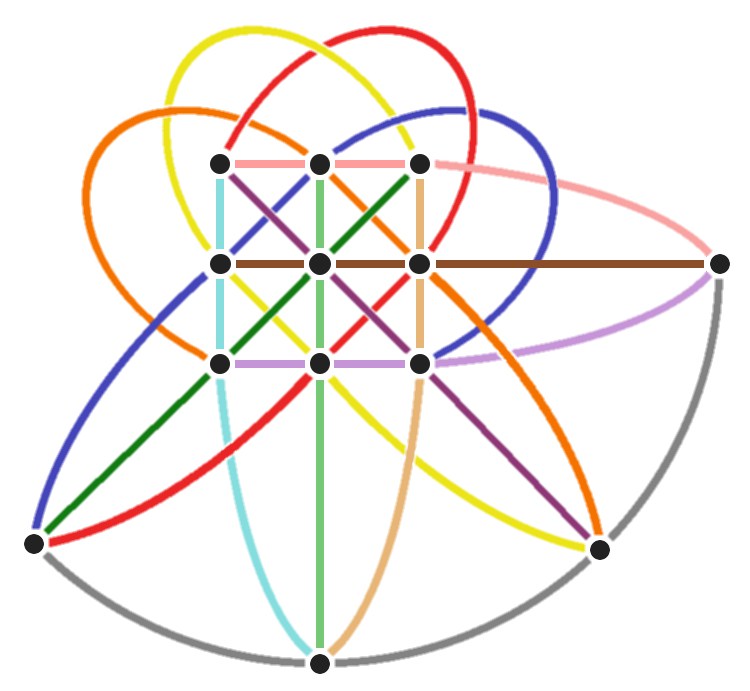
Ha egy 13 lapos Dobble-paklit szeretnénk megtervezni, akkor a leggyorsabb megoldás, ha ezt a harmadrendű síkot feleltetjük meg a paklinak. Minden egyenes egy figurát, minden pont egy lapot jelent. Például a “legjobboldalibb” pont az a lap lenne, amin a barna, szürke, rózsaszín és halványlila színnel jelölt figurák lennének.
a kép forrása: puzzlewocky.com
A beszélgetés során okosan, taktikusan elkerüljük a matematikai mélyvizeket. Megnézzük, hogy hol vannak, summázzuk, hogy igen mélyek, de nem ugrunk beléjük egyszer sem, nem ez a cél. Sokkal inkább, hogy jöjjünk össze egy kicsit a matematika égisze alatt, jöjjünk rá, hogy nem olyan borzasztó dolog ez, és talán nincs annyira messze a mindennapoktól, a képzelettől, mint gondoljuk. Az esemény végén egy kis kötetlen beszélgetés végtelenekről és végességről, aztán taps, és mint egy nagycsaládi ebéd végén, mindenki segít rendet rakni a szobában, mielőtt hazaindulna.
A kiemelt kép forrása az esemény facebook oldala

